(ENEM 2019 PPL) Um fiscal de certa empresa de ônibus registra o tempo, em minuto, que um motorista novato gasta para completar certo percurso. No Quadro 1 figuram os tempos gastos pelo motorista ao realizar o mesmo percurso sete vezes. O Quadro 2 apresenta uma classificação para a variabilidade do tempo, segundo o valor do desvio padrão.
Quadro 1

Quadro 2
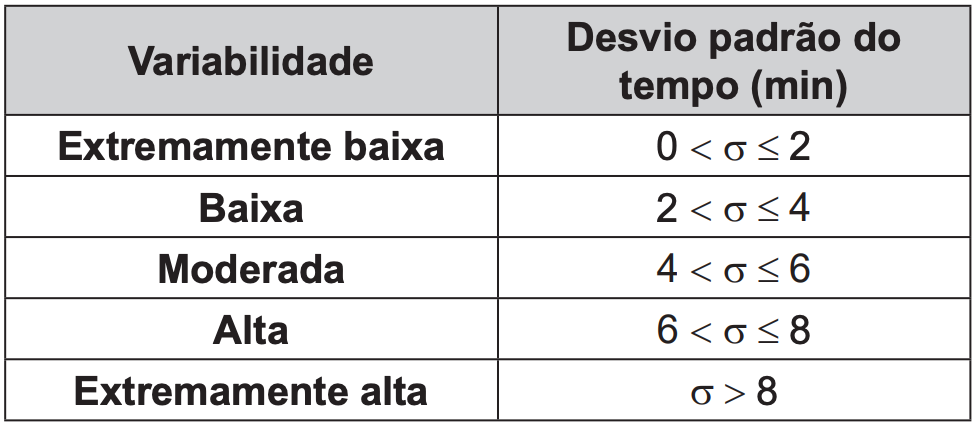
Com base nas informações apresentadas nos quadros, a variabilidade do tempo é
A extremamente baixa.
B baixa.
C moderada.
D alta.
E extremamente alta.
Dicas e Resolução
Dica 1
Temos que calcular o desvio padrão dos números do quadro 1. Vamos ver como faz isso passo a passo.
O primeiro passo é você calcular a média aritmética dos números do quadro 1.
Vamos lá, agora é a sua vez!
Resolução da Dica 1
\(\frac{48+54+50+46+44+52+49}{7}\)
\(=\frac{343}{7}=49\)
A média aritmética dos números do Quadro 1 vale 49
Dica 2
Agora, temos que calcular a diferença de cada número do quadro em relação à média de 49.
Por exemplo, vamos calcular a diferença do primeiro número 48 em relação à média 49
48 – 49 = -1
A diferença do primeiro número 48 em relação à média 49 deu -1
Agora, vamos repetir o mesmo procedimento para todos os números do Quadro 1
Resolução da Dica 2
| Tempo (min) | Diferença em relação à média 49 | |
| 48 | 48 – 49 = -1 | |
| 54 | 54 – 49 = 5 | |
| 50 | 50 – 49 = 1 | |
| 46 | 46 – 49 = -3 | |
| 44 | 44 – 49 = -5 | |
| 52 | 52 – 49 = 3 | |
| 49 | 49 – 49 = 0 |
Dica 3
Agora, o próximo passo é calcularmos as diferenças ao quadrado.
Por exemplo, na primeira linha da tabela acima, a gente calculou que a diferença é -1. Então a diferença ao quadrado vale (-1) x (-1) = 1
Mais um exemplo, na segunda linha, a diferença deu 5. A diferença ao quadrado fica 5 x 5 = 25.
Vamos repetir essa mesma lógica para toda a tabela.
Resolução da Dica 3
| Tempo (min) | Diferença em relação à média 49 | Diferença ao quadrado |
| 48 | -1 | (-1) x (-1) = 1 |
| 54 | 5 | 5 x 5 = 25 |
| 50 | 1 | 1 x 1 = 1 |
| 46 | -3 | (-3) x (-3) = 9 |
| 44 | -5 | (-5) x (-5) = 25 |
| 52 | 3 | 3 x 3 = 9 |
| 49 | 0 | 0 x 0 = 0 |
Dica 4
O próximo passo é calcularmos a média artimética das diferenças ao quadrado.
Então, temos que calcular a média aritmética dos números da última coluna.
Resolução da Dica 4
\(\frac{1+25+1+9+25+9+0}{7}\)
\(=\frac{70}{7} = 10\)
A média aritmética das diferenças ao quadrado vale 10
Dica 5
Agora, finalmente vamos para o desvio padrão.
O desvio padrão é a raiz quadrada da média das diferenças ao quadrado.
Ou seja, o desvio padrão é a raiz quadrada do valor que calculamos na dica anterior.
Então, o desvio padrão \(\sigma = \sqrt{10}\)
O valor \(\sigma = \sqrt{10}\) se encaixa em qual das classificações do Quadro 2 do enunciado?
Resolução da Dica 5
Sabemos que \(3^2 = 9\) e que \(4^2 =16\)
Como 10 é um número que fica entre 9 e 16, então \(\sqrt{10}\) é um número entre 3 e 4.
Então nossa conclusão é que o desvio padrão \(\sigma\) é um número entre 3 e 4.
A classificação Baixa do Quadro 2 indica que \(2 \lt \sigma \le 4\). Mas, isso é verdade. Vimos que \(\sigma\) está entre 3 e 4. Logo, \(\sigma\) também está entre 2 e 4.
A variabilidade do tempo é Baixa.
Resposta
Alternativa B
Convite para o nosso Grupo de Estudos no Telegram
Olá, gostaria de te convidar para o nosso grupo de estudos no Telegram. Pelo grupo, a nossa comunicação ficará um pouco mais fácil. Vamos discutir e resolver questões de provas passadas e vamos conversar sobre a sua preparação para o ENEM e os vestibulares. E claro, você poderá me enviar as suas dúvidas!
Para entrar no grupo, basta clicar no botão abaixo. Abs! Prof. Henry

Listas de Exercícios (focadas no ENEM)
Preparei uma série de listas de exercícios de Matemática focados no ENEM. Você terá uma lista para cada assunto de Matemática que aparece no ENEM.
Os exercícios nas listas estão ordenados por nível de dificuldade, começando nos mais fáceis, até os mais difíceis. Além disso, todas as questões são de provas anteriores do ENEM e de vestibulares.
O melhor de tudo é que para cada exercício você terá dicas e a resolução detalhada.
O grande objetivo dessas listas é que você se prepare bem para ficar craque em questões do nível do ENEM.


